一道带有遗憾的算法题
前言
最近面试一个非常心仪的职位,结果跪在一道算法题目上,让我几晚都睡不着,翻来覆去。面试失败后回去,结果当晚花了不到十分钟就解决了这个看似很难,实际上非常简单的题目。现在已经过去了,总结下这个问题,顺便给博客开了算法模块。
题目
有一个N层的金字塔,第一层(最顶层)有一个格子,第二层有2个格子,第三层有3个格子,第N层有N个格子,如图
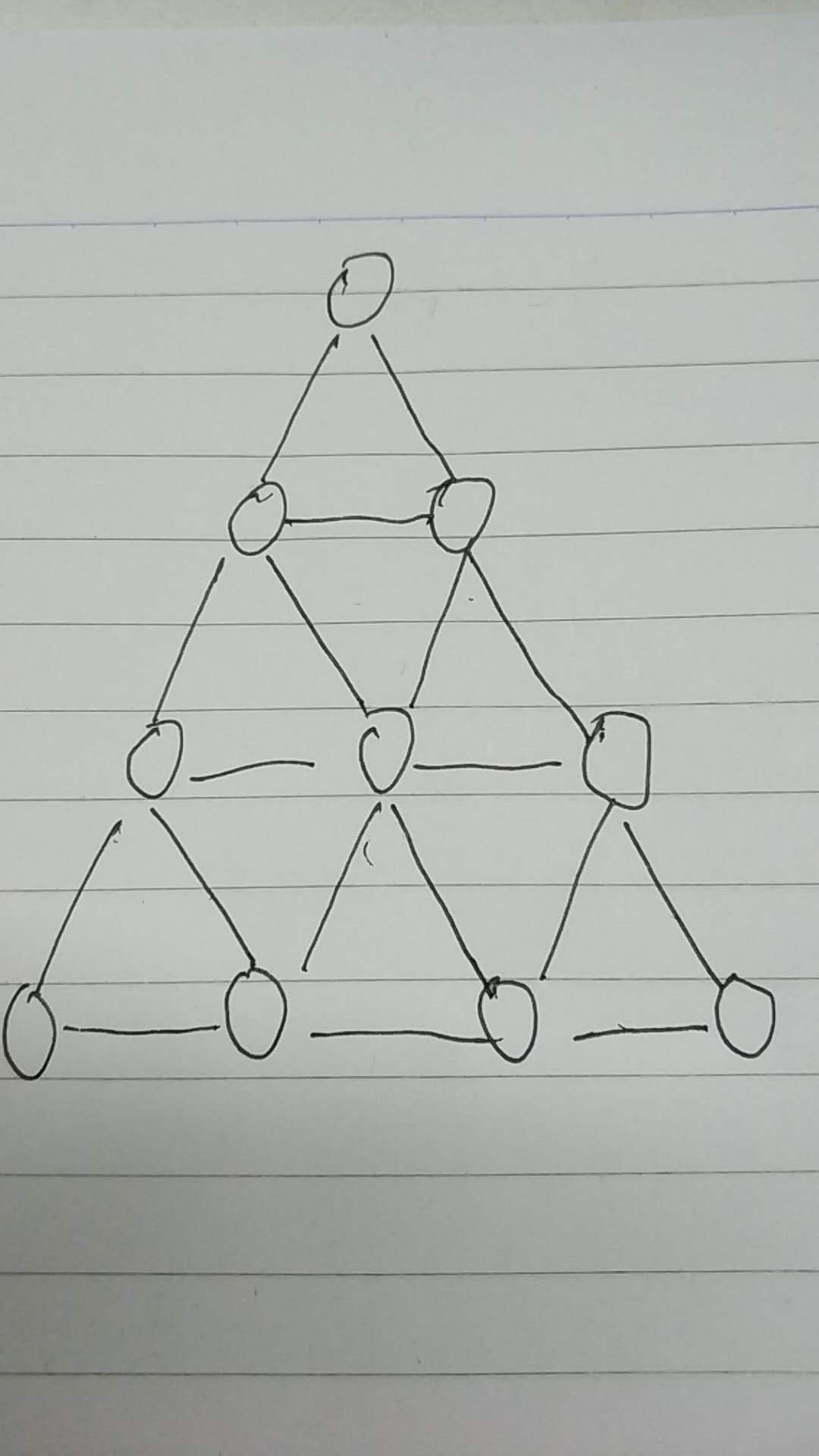
现有3种不同的颜色,对所有的格子进行填充,要求每相邻的格子的颜色不能相同。
分析
在做这道题目的时候,面试官曾经给过很好的提示,就是找到它的规律。其实这句话已经很明显了,现在回头想想,我们多画几层看看,就知道最终的结果到底能带出什么规律了。
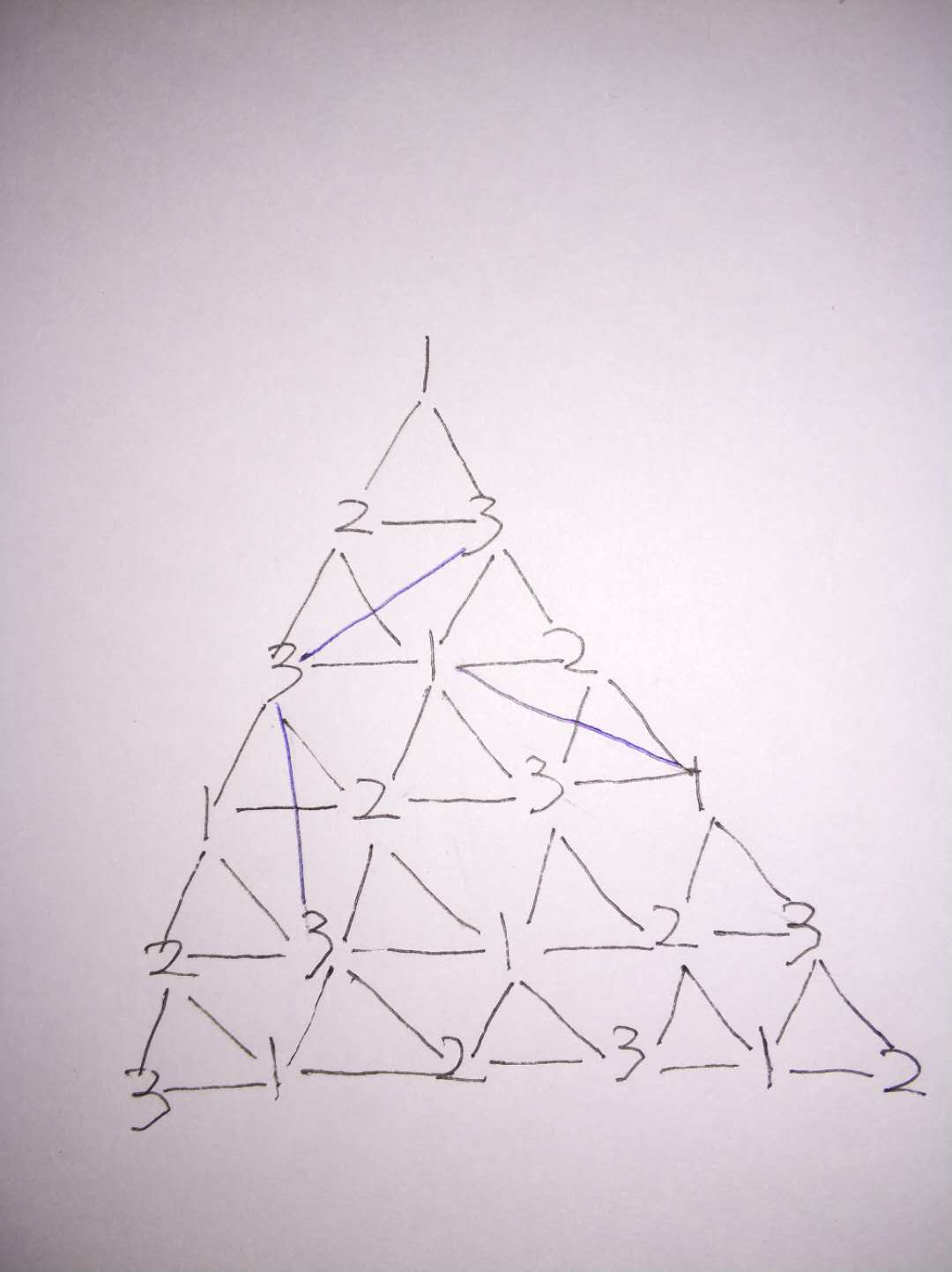
总的规律就是
1.确定前2层的三个节点后,就能确认下面所有层的节点填充的颜色
2.每一层的第一个跟斜上角的节点填充的颜色一致
3.每一层最后一个节点填充颜色跟左斜上角的一致
4.中间部分节点颜色跟顶上的对角的颜色一致
具体看上面那个图的蓝色线条部分画出的对角线。所以就是这样,非常简单,规律也很简单。
实现
面试还犯了一个严重的错误就是,这个金字塔到底是采用什么数据结构存储,我以为是树节点,但是树节点是完全满足不了的,中间的节点会有N个关联的节点,完全存储不了。其实根据金字塔的结构,用二维数组是最好的方式。
代码实现如下,java版本:
public class ALG {
public static void main(String[] args) {
int length = 20;
int[][] arr = new int[length][length];
for (int i = 0; i < length; i++) {
if (i == 0) {
arr[i][0] = 1;
} else if (i == 1) {
arr[i][0] = 2;
arr[i][1] = 3;
} else {
for (int j = 0; j <= i; j++) {
// 第一个跟斜上角的参数的值一致
if (j == 0) {
arr[i][j] = arr[i - 1][j + 1];
} else if (j == i) {
//最后一个跟左斜上角的一致
arr[i][j] = arr[i - 1][j - 2];
} else {
// 中间那个跟顶上的对角的一致
arr[i][j] = arr[i - 2][j - 1];
}
}
}
}
// 输出
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr[i].length; j++) {
if (arr[i][j] > 0) {
if (j == 0) {
System.out.print(getSpace(i, arr.length));
}
System.out.print(arr[i][j] + " ");
}
}
System.out.println(" ");
}
}
private static String getSpace(int index, int length) {
StringBuilder builder = new StringBuilder("");
for (int i = 0; i < length - index; i++) {
builder.append(" ");
}
return builder.toString();
}
}
输出效果如下: